

🔬 Research Summary by Ozgur Guldogan, Yuchen Zeng, Jy-yong Sohn, Ramtin Pedarsani, and Kangwook Lee
Ozgur Guldogan is a Ph.D. student at the University of California, Santa Barbara. His research interests are fairness, differential privacy, and federated learning.
Yuchen Zeng is a Ph.D. candidate at the University of Wisconsin-Madison, working on model fairness, large language models, federated learning, and differential privacy.
Jy-yong Sohn is a post-doctoral researcher at the University of Wisconsin-Madison, and he is interested in the intersection of machine learning, information theory, and distributed algorithms.
Ramtin Pedarsani is an associate professor at the University of California, Santa Barbara. His research interests are broadly in the areas of machine learning, optimization, coding, and information theory.
Kangwook Lee is an Assistant Professor at the University of Wisconsin-Madison, and his research interests lie in machine learning, deep learning, information theory, and coding.
[Original paper by Ozgur Guldogan*, Yuchen Zeng*, Jy-yong Sohn, Ramtin Pedarsani, and Kangwook Lee]
Overview: Devising a fair classifier that does not discriminate against different groups (e.g., race, gender, and age) is an important problem in machine learning. However, most existing fairness notions focus on immediate fairness and ignore their potential long-term impact. In contrast, we propose a new fairness notion called Equal Improvability (EI), which aims to equalize the acceptance rate across different groups when each rejected sample tries to improve its feature.
Introduction
It has been observed that machine learning approaches are unfair to individuals having different ethnicity, race, and gender. Various fairness notions and fair learning algorithms have been suggested over the past decade to address this issue. However, most of the existing fairness notions only focus on immediate fairness without taking the potential follow-up inequity risk into consideration. Recently, a few fairness methods are capturing the potential follow-up effect notions that have been proposed, but they suffer from various limitations.
In this paper, we propose a new group fairness notion called Equal Improvability (EI), which aims to equalize the probability of rejected samples being qualified after a certain amount of feature improvement for different groups. EI encourages rejected individuals in different groups to have equal motivation to improve their features to get accepted in the future. We analyze the properties of EI and the connections of EI with other existing fairness notions and provide three methods to find a fair classifier in terms of EI. Our experiment shows two things: (i) the proposed algorithms achieve EI fairness, and (ii) achieving EI can reduce the gap between the distributions of groups in the long run.
Key Insights
Motivation
In the left figure, we provide an example to illustrate why considering the potential follow-up risk is essential. Assume two groups, Group 0 and Group 1. The decision boundary shown in the figure accepts 50% of the samples from both groups. This decision boundary is fair in terms of Demographic Parity (DP), which requires the acceptance rate of different groups to be equal. However, we notice that the rejected samples (left-hand-side of the decision boundary) in group 1 are located further away from the decision boundary than the rejected samples in group 0. As a result, the rejected applicants in Group 1 need to make more effort to cross the decision boundary and get approval. This improvability gap between the two groups can make the rejected applicants in Group 1 less motivated to improve their features, which may increase the gap between different groups in the future.
Definition of Equal Improvability
Motivated by the above example, we introduce our new fairness notion: Equal Improvability (EI). Consider a score-based classifier f, which accepts the sample with the feature x if f(x)0.5, and rejects the sample otherwise. Let each sample can improve its features by a certain amount , and let z be the index of the group to which the sample belongs to. The condition for EI is written as
P(||x|| f(x+x)0.5 | f(x)<0.5, z =0) =P(||x|| f(x+x)0.5 | f(x)<0.5, z=1).
In other words, EI requires the improvability of the reject samples from different groups to be the same, which eliminates the concerns raised by most existing fairness notions considering immediate fairness.
Achieving Equal Improvability
We propose to achieve equal improvability by formulating fairness-regularized optimization problems with differentiable objective functions. Then, one can leverage common gradient descent algorithms to train a fair model in terms of EI. We introduce three ways to formulate the EI unfairness as a differentiable function of the model parameters. They are covariance-based, kernel density estimation (KDE)-based, and loss-based, respectively.
Experiments
We first evaluate the performance of our proposed approaches in mitigating EI unfairness. We employ an empirical risk minimizer (ERM) as the baseline here. The following table shows that our proposed approaches can significantly reduce the unfairness in terms of EI while maintaining low error rates.
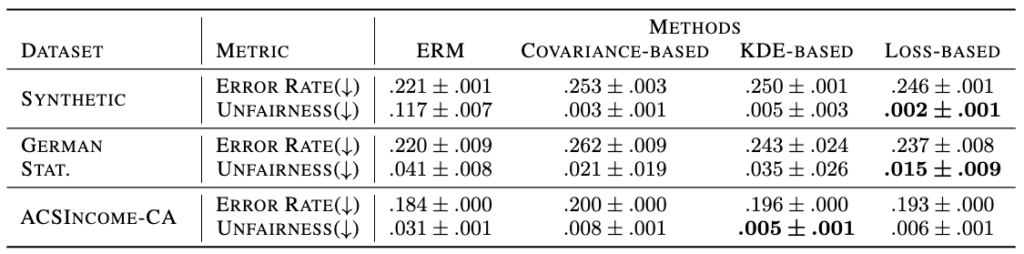
Moreover, we study how EI affects long-term unfairness, which is measured by the gap between the distributions of different groups. In this experiment, we include three other fairness notions as baselines: Demographic Parity (DP), Bounded Effort (BE) [1], and Equal Recourse (ER) [2]. We formulate a dynamic system to model how individuals respond to the decision boundary and how data distribution changes. We consider multiple iterations of the following procedure: given a decision rule (ERM or particular fairness requirement), at each iteration, we (i) first compute the classifier given the requirement based on the current data distribution and then (ii) update the data distribution based on the obtained classifier. The evolution of long-term unfairness resulting from different decision rules is reported in the figure below. We observe that the long-term unfairness of the EI classifier reduces faster than other existing fairness notions, showing that EI proposed in this paper helps achieve long-term fairness.

Between the lines
This paper discusses the importance of considering the long-term impact while defining fairness notions. We expect our work sheds light on research topics for encouraging minority groups to improve their features and thus reduce the true qualification gap with majority groups. Moreover, we hope our new fairness notion can be used in fairness-sensitive real-world applications so that different groups have similar quality distribution in the long run.
Since the “far-sighted” fairness notions (including our EI fairness notion) are recently proposed in the research community, many exciting problems remain in this field. First, due to the complexity of the theoretical analysis in the dynamic scenarios, we only provided empirical results showing that EI can mitigate long-term fairness. Thus, mathematical analysis on the impact of far-sighted fairness notions in dynamic scenarios remains an interesting open problem. Second, our dynamics system only considers binary demographic groups and one-dimensional features. Extending our work to settings with multiple sensitive attributes and high-dimensional features remains a future direction. Finally, our proposed dynamic system does not aim to capture all the behavioral nuances involved perfectly. Therefore, our model might not perfectly mimic the real scenario. We leave performing human studies to explore the limitations of the proposed system as one of the interesting follow-up works.
References
[1] Hoda Heidari, Vedant Nanda, and Krishna P. Gummadi. On the long-term impact of algorithmic decision policies: Effort unfairness and feature segregation through social learning, 2019.
[2] Von Kügelgen, Julius, Amir-Hossein Karimi, Umang Bhatt, Isabel Valera, Adrian Weller, and Bernhard Schölkopf. On the fairness of causal algorithmic recourse. In Proceedings of the AAAI Conference on Artificial Intelligence, vol. 36, no. 9, pp. 9584-9594. 2022.
