
🔬 Research Summary by Stephen Fitz, an Artificial Intelligence scientist working in the areas of Neural Networks, Representation Learning, and Computational Linguistics.
[Original paper by Stephen Fitz]
Overview: We develop a novel approach to visualize moral dimensions within language representations induced by Large Language Models (LLMs) such as those underlying ChatGPT. Results of our analysis suggest that GPT-based AI systems trained on natural language data develop a natural understanding of fairness. Our method does not rely on model outputs but can detect that ability by analyzing the topological structure of internal representations induced by its neural networks.
Introduction
Since the release of ChatGPT, and subsequently GPT-4, there has been an increased interest in AI safety and alignment research. As Large Language Models (LLMs) are deployed within Artificial Intelligence (AI) systems that are increasingly integrated with human society, studying their internal structures becomes more important than ever. Higher level abilities of LLMs such as GPT-3.5 emerge largely due to informative language representations they induce from raw text data during pre-training on trillions of words. These embeddings exist in vector spaces of several thousand dimensions, and their processing involves mapping between multiple vector spaces with a total number of parameters on the order of trillions. Furthermore, these language representations are induced by gradient optimization, resulting in a black box system that is hard to interpret. In this paper, we take a look at the topological structure of neuronal activity in the “brain” of ChatGPT’s foundation language model and analyze it concerning a metric representing the notion of fairness.
We first compute a fairness metric inspired by social psychology literature to identify factors that typically influence human fairness assessments, such as legitimacy, need, and responsibility. Subsequently, we summarize the manifold’s shape using a lower-dimensional simplicial complex, whose topology is derived from this metric. We color it with a heat map associated with this fairness metric, producing human-readable visualizations of the high-dimensional sentence manifold.
Our results show that sentence embeddings based on GPT-3.5 can be decomposed into two submanifolds corresponding to fair and unfair moral judgments. This indicates that GPT-based language models develop a moral dimension within their representation spaces and induce an understanding of fairness during their training process.
Key Insights
Introduction
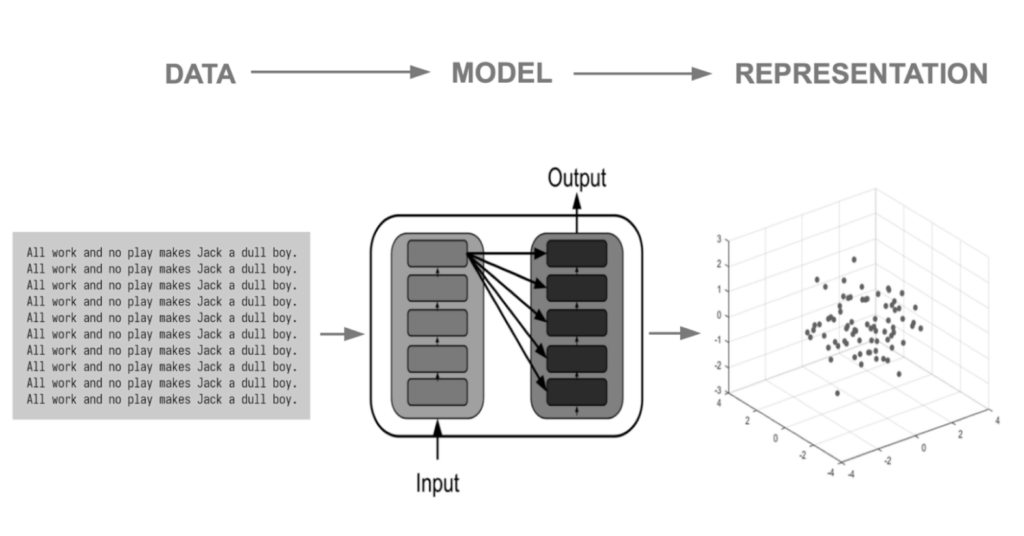
Large transformer language models develop their understanding of sentences by inducing informative vector space representations of linguistic units within their neural activations. The above figure summarizes this idea. The base language model transforms a text corpus into a point cloud of vectors. This induces an implicit embedding of any text into a submanifold of a high dimensional ambient vector space, whose metric is learned in a self-supervised fashion by backpropagation gradient descent on large amounts of text extracted from the internet. The topology and geometry of that vector space allow AI assistants such as ChatGPT to perform their cognitive functions. (The figure above shows the point cloud in 3D for visualization purposes, while the manifold we analyze in this study is embedded within a much larger space with more than a thousand dimensions.)
In this paper, we probe the topological structure of vector space representations of sentences induced by GPT-3.5 – the foundation language model behind ChatGPT to gauge its understanding of moral values. For this purpose, we introduce novel approaches from computational algebraic topology to studying LLMs. We compute a metric of fairness based on prior studies in computational social sciences and use it to perform a topological summary of a 1536-dimensional sentence embedding manifold with a one-dimensional simplicial complex (i.e., a graph) whose vertices correspond to clusters of sentence representations under a projection onto a “fairness” dimension, and edges to pairwise cluster intersections. This procedure produces a sketch of the original high-dimensional manifold (which is impossible to visualize directly) with a topological object that can be visualized in human-readable form. Furthermore, the shape of the resulting visualization gives clues about the general shape of the representation space of the language model. We also produce a heat map with colors corresponding to the degree of fairness. This coloring allows us to inspect the manifold for separation into submanifolds corresponding to fair vs unfair moral judgments. We observe a clear separation pattern, which suggests the notion of fairness is encoded in the shape of the high dimensional representation manifold induced by the language model.
Fairness Metric
After delving deep into the psychology literature to identify factors that influence humans’ fairness assessments, we developed an approach that allows us to harness implicit social biases in language, producing a procedure for an explainable assessment of sentences related to fairness.
Because large GPT models are trained in autoregressive fashion on trillions of tokens of text, the metric they induce in the sentence representations encodes various features of natural language sentences, including semantics and moral judgments. This translates to the inner product within those spaces expressing similarity across multiple aspects of natural language. Convex combinations of sentence embeddings can express a semantic gradient between the chosen concepts expressed by these sentences. Very large language models like GPT-3.5 induce surprisingly powerful sentence representations, leading to the observed emergent properties of these models. If we consider vector space representations of sentences “it was beneficial” and “it was harmful” and compare them to a representation of a test sentence, such as “the guard helped the man” by computing cosine similarity, the result will be a score in the interval [-1,1]. The more associated the sentence is with benefit, the closer to 1 this normalized inner product tends to be. In contrast, sentences that are more associated with harmfulness will provide an outcome closer to -1.
Our technique is inspired by this idea. It is based on five factors representing concepts of responsibility, pleasure, benefit, reward, and harm. In our computation, every factor is derived from pairs of sentences representing two polarities of each factor. The vector representations are obtained from stimulating neurons of the transformer encoder blocks within GPT3.5 by a set of several hundred examples of sentences representing fair vs. unfair moral situations according to human feedback.
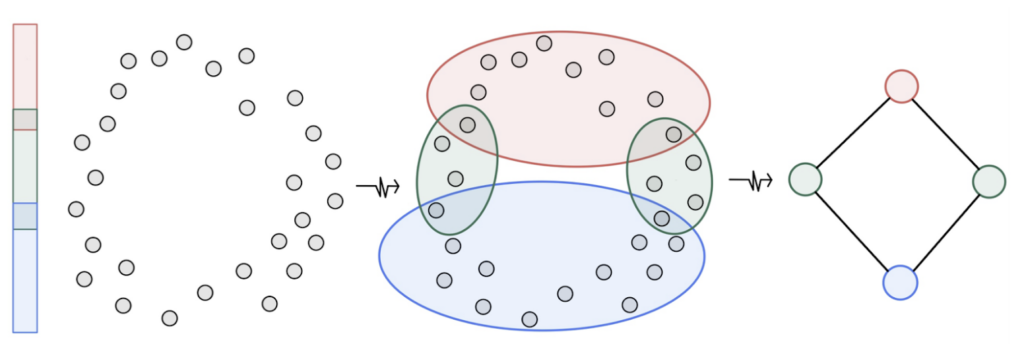
The figure above gives a low-dimensional explanation of the method used to analyze GPT’s moral dimensions. In this example, we induce topological structure from a point cloud representing noisy samples from a neighborhood of a 1-dimensional submanifold of a 2-dimensional vector space. The resulting topological representation (a simplicial complex) is a graph with four vertices corresponding to clusters of the projection on the left and four edges corresponding to their intersections in the original embedding space. Note that the object obtained is topologically equivalent to a circle and gives a reasonable summary of the shape of this original 2D point cloud of vectors.
The technique we use to study GPT-3.5’s sentence embeddings is a topological dimensionality reduction method, where the goal is to summarize the shape of our representation space with a rough sketch in the form of a low-dimensional topological manifold.
This reduced representation can be considered a map approximating the shape of our embedding space. A human can visually inspect such a description while remaining more topologically informative than a naive projection. Instead of studying the high dimensional vector space representations of language within GPT directly, we can map them to a different space first, define an open cover, and then cluster the original points within the preimage of each cover set. This produces a summary of the topological features in the embedding with a simplicial complex of a chosen dimension. In particular, we generated 1-dimensional simplicial complexes (i.e., graphs) from GPT-3.5-based sentence representations by projecting them onto the fairness dimension and then analyzing clusters of original high-dimensional sentence embeddings concerning an open cover of that projection. We also applied a coloring according to a heat map corresponding to the magnitude and sign of that projection. The resulting data structure allows for a visual exploration of the shapes of these high-dimensional embedding manifolds to identify the distribution of fairness in the representation space.
Results
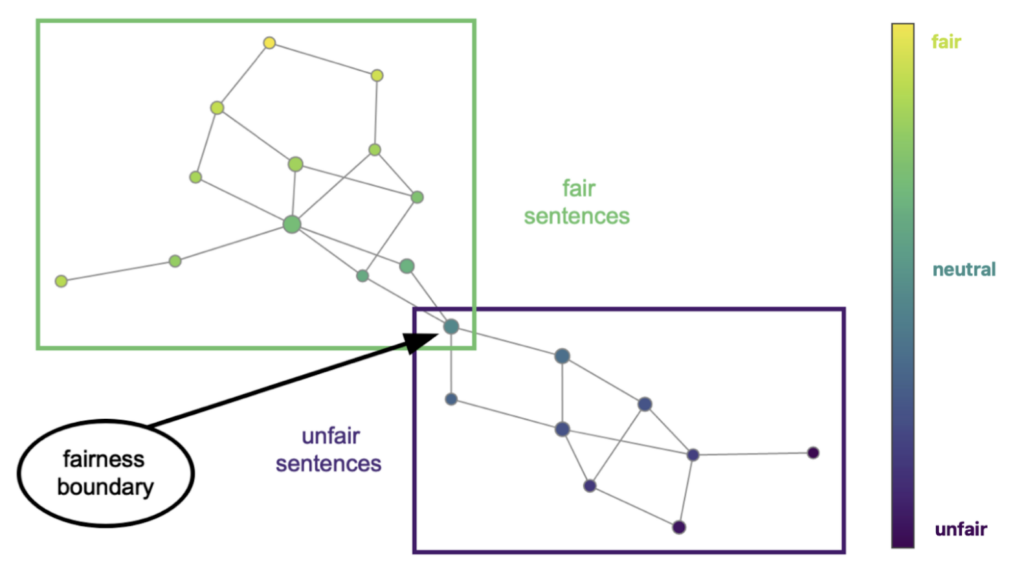
Visualization in the figure above shows the results of applying our method to a 1536-dimensional vector space representations of sentences obtained from GPT-3.5-based embedding model. The fairness subspace clearly subdivides the 1536-dimensional representation space within the GPT-3.5 language model into two submanifolds. When the language model is prompted with fair sentences, different patterns of neuronal activation are manifested within the transformer layers than when the model is prompted with morally unfair examples. This leads to the sentence representation manifold being separated into submanifolds corresponding to these two extremes. Each part is itself a topologically complex space, but the two parts are linked in a single cluster of morally ambiguous sentences. The sentences in the green part of the manifold are all judged fair, while all the sentences in the blue part represent unfair situations.
Its emergent abilities to judge the fairness of situations are partially enabled by the topological structure of this embedding manifold. Each node corresponds to a cluster of sentences obtained by first projecting their embeddings onto the fairness subspace defined earlier in this paper and then grouping the original sentences based on preimages of an open cover of this projection. This procedure gives a topological sketch of the general shape of this high-dimensional sentence representation manifold. Node sizes are defined in proportion to the number of sentences in each cluster. Their colors are based on the heat map shown to the right, which is a gradient corresponding to the sign and magnitude of the projection. High values on that scale correspond to fair, while low values to unfair situations (as described by the sentences). The edges come from cluster intersections in the original high-dimensional space and thus give visual cues to how the clusters are distributed within the embedding manifold
We see that each box bounds a topologically complex manifold (due to the nontrivial pattern of edges), but no edges connect nodes from different boxes. This means the entire manifold comprises two submanifolds corresponding to fair and unfair situations. This separation of colors suggests that there are subregions in this high dimensional representation space corresponding to activation patterns within the encoder neural network that occur only when fair sentences are processed and separate disconnected regions corresponding to neural activations caused by unfair sentences.
Between the lines
The behavior of these models is determined by the vector space representations of inputs they induce from text during training. Therefore, the existence of clear patterns in the shape of those representation manifolds, such as separation into regions corresponding to moral aspects of language, can serve as a tool to examine their abilities intrinsically. This is in contrast to the mainstream approaches that are currently used, which are extrinsic and behavioral. In these contemporary approaches, the abilities of the model are examined with techniques based on prompting and analyzing the outputs or by proxy of performance on downstream tasks. The approach presented here is novel in the field of AI and NLP in particular.
It is more analogous to performing studies on the brain with something like fMRI or a Neuralink device and analyzing topological patterns in neural communication to study the subject instead of making judgment based on the subject’s apparent behavior or reports from introspection. This alternative way of looking at language models could benefit alignment research and AI safety, and we hope this paper serves as an inspiration for the community to develop more tools of this kind.
