

🔬 Research Summary by Faisal Hamman, a Ph.D. student at the University of Maryland, College Park. Faisal’s research focuses on Fairness, Explainability, and Privacy in Machine Learning, where he brings novel foundational perspectives from information theory, statistics, and optimization.
[Original paper by Faisal Hamman and Sanghamitra Dutta]
Overview: This research presents an information-theoretic formalization of group fairness trade-offs in federated learning (FL) where multiple clients come together to collectively train a model while keeping their own data private. A critical issue that arises is the disagreement between global fairness (overall disparity of the model across all clients) and local fairness (disparity of the model at each client), particularly when the data distributions across each client are different with respect to sensitive attributes such as gender, race, age, etc. Our work identifies three types of disparities—Unique, Redundant, and Masked—contributing to these disagreements. It presents theoretical and experimental insights into their interplay, answering pertinent questions like when global and local fairness agree and disagree.
Introduction
As machine learning permeates high-stakes sectors like finance, healthcare, recommendation systems, etc., ensuring these algorithms are fair becomes increasingly crucial. This issue is especially complex in the federated learning setting, where several clients collaborate to develop a machine learning model without directly sharing their datasets. For instance, several banks may work together to develop a credit assessment model but are legally prohibited from sharing customer data amongst themselves.
In the traditional single-node machine learning scenario, numerous techniques exist to ensure group fairness (individuals are treated equally, irrespective of their sensitive attributes such as race, gender, age.) However, these techniques falter in federated learning settings, mainly due to the decentralized nature of data and the training process because each client only has access to their own data. In real-world scenarios, local population demographics can differ significantly from global demographics (i.e., a bank branch having customers who are predominantly from a particular race). Despite this, most existing studies have primarily focused on either global fairness – the overall disparity of the model across all clients, or local fairness – the disparity at each client’s level, without delving much into their interplay or trade-offs.
This paper presents an information-theoretic perspective on group fairness trade-offs in federated learning (FL). We leverage a body of work in information theory called partial information decomposition (PID) to identify three distinct types of disparity that constitute the global and local disparity in FL: Unique, Redundant, and Masked Disparity. This decomposition helps us derive fundamental limits and trade-offs between global and local fairness, particularly under data heterogeneity, as well as derive conditions under which they would fundamentally agree or disagree with each other.
Key Insights
FL has two group fairness notions: Global Fairness and Local Fairness. Global fairness ensures that the model doesn’t discriminate against any protected group when evaluated across all client’s data. Meanwhile, local fairness focuses on fairness within each client’s data. These types of fairness often conflict due to data heterogeneity among clients or different demographics at the local and global levels. For instance, consider a case involving three banks: Bank A, predominantly serving an older population; Bank B, catering to a diverse demographic; and Bank C, primarily serving a younger clientele. Achieving global fairness, where the model performs equitably across combined data from all banks, might necessitate compromises on local fairness within each bank’s specific demographic and vice versa.
Most existing research on group fairness in FL focuses on global or local fairness, often neglecting the critical interplay between these two dimensions. This has led to a widespread gap in understanding how these concepts relate to each other within different contexts, potentially leading to the development/deployment of algorithms that may fail to achieve global and local fairness, often compromising one for the other. Our focus is on understanding the fundamental limits that can be achieved by any strategy given a particular data distribution.
Our paper formalizes the notions of group fairness in FL by adopting an information-theoretic approach to quantify these disparities. Information theory is a powerful tool in this context, allowing us to rigorously quantify these disparities and identify fairness tradeoffs in FL. Global Disparity is defined as the mutual information between the model’s decision and the sensitive attribute. In simple terms, mutual information evaluates the extent of dependence between two variables. For instance, if the model’s predictions are highly correlated with sensitive attributes (like gender or ethnicity), that’s a sign of potential unfairness. Local Disparity can then be represented as conditional mutual information, which is the dependence between the model’s decision and sensitive attributes conditioned on a specific client.
We draw upon a specialized area of information theory known as Partial Information Decomposition (PID) to identify three distinct types of disparity that contribute to global and local disparity in FL: Unique, Redundant, and Masked Disparity.
Our work is the first to identify that the unique and redundant disparities constitute the global disparity while the unique and masked disparities constitute the local disparity. We visualize this as a Venn diagram below.
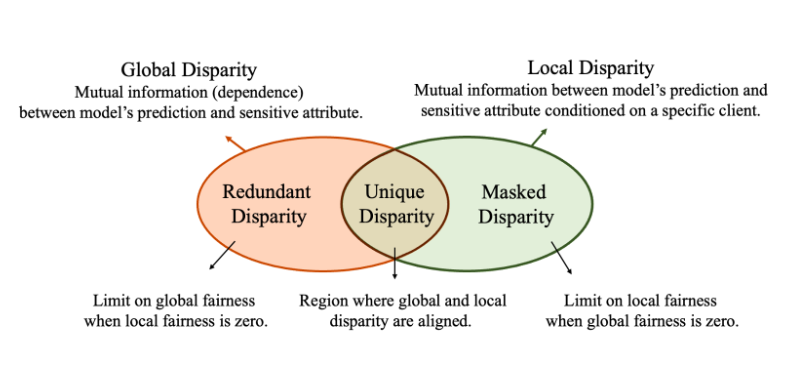
To better understand these concepts, consider canonical examples with binary-sensitive attributes across two participating clients.
Unique Disparity captures information about sensitive attributes that one can get from predictions that are not due to the client. For example, assume men and women are equally distributed across two clients, so there is no dependence between client and gender. However, a model only approves men but rejects women for a loan across both clients. This highlights a case of unique disparity since all the information about the sensitive attribute (gender, in this case) is derived exclusively from the predictions, irrespective of the clients. Such a model would be globally and locally unfair because the model’s decisions are exclusively based on the sensitive attribute of gender, disregarding any other factors.
Redundant Disparity captures the information about the sensitive attribute that is present in both the model’s predictions and the clients. Consider two clients: one predominantly catering to women (say a 90-10 female-to-male ratio) and the other primarily serving men (say a 10-90 female-to-male ratio), so there is a correlation between the clients and gender. Take a model that approves everyone from the first client while rejecting everyone in the second. Such a model is fair within each client—locally fair—because men and women are treated equally within a particular client. However, the model is globally unfair when viewed across all clients.
Masked Disparity captures an interesting scenario: the “synergistic” information about the sensitive attribute that becomes apparent only when considering both the model’s predictions and the client but is not present in any one of them individually. For instance, both men and women are evenly distributed across two clients. A model only approves men from one client and only women from the other client while rejecting everyone else. Such a model is locally unfair, as it singularly prefers one gender within each client. However, it is globally fair, since it maintains an equal approval rate for both men and women globally. Here, the local unfairness at each client is evens out to achieve global fairness.
We uncover the fundamental information-theoretic limits and trade-offs using the PID decompositions of global and local disparity. For instance, we’ve found that focusing solely on local fairness—ensuring each client’s model is fair—can be convenient but may not lead to a globally fair model. This is particularly true when there’s redundant disparity. Even though each client’s model might seem fair within its own dataset, it doesn’t guarantee that the combined model will be fair when applied across all clients.
Conversely, even if a model is designed to be globally fair, it doesn’t necessarily mean it will be fair when implemented at the local client level. This limitation arises due to the masked disparity. A model that looks fair when considering all clients but might have biases when evaluated at each client. This is a significant concern, as models are often deployed at the local client level.
The paper also provides the scenarios where focusing on one type of fairness will naturally lead to the other, i.e., specific scenarios where ensuring fairness at the local level will also result in a globally fair model and vice versa.
Between the lines
Our research offers an in-depth exploration of the intricacies of fairness within the FL setting. By identifying the specific types of disparities that contribute to unfairness and outlining the inherent trade-offs between global and local fairness and between fairness and model accuracy, we provide a nuanced framework that could serve as a foundation for more effective and fair federated learning applications. Understanding the fundamental limits is vital, as it helps delineate the optimal performance any algorithm can achieve within the specified problem setting. PID terms allow one to delineate regions of agreement and disagreement between global and local fairness alongside the necessary trade-offs with model accuracy.
The methodology could extend to encompass a wider array of fairness metrics, such as equalized odds, etc., fostering a richer and more comprehensive understanding of fairness in complex settings. Moreover, it spearheads the development of various practical and efficient algorithms designed to mitigate biases in the FL setting.
The work not only fills existing gaps in understanding fairness in FL but also prompts critical questions for ongoing research and fosters policy discussions that set the stage for more robust, fair, and accurate models under distributed and federated settings.
